Square waveform generator
On the following three-part tutorial, a square waveform generator is presented.
The requirements for the project are to generate a sequence of square waveforms with different frequencies. For each frequency a number of cycles is generated (different for each one). For each frequency, a distinct duty cycle is also defined.
In this implementation the frequency is defined in Hz., and the active high time in ns. The VHDL code does not validate the parameters, i.e, if the active high time for any frequency is longer than its period, the output will be always '1' for that frequency. For each frequency, a number of cycles is defined.
This project was born over a discussion in Xilinx forums. Once I did the project for a specific configuration I started thinking about a way to make a generic solution, and this tutorial tries to reflect the design process of this small project.
The code is presented below. Three different frequencies FREQ1..3 are defined for this example, 242KHz, 23kHz and 57kHz. Notice that each frequency is defined in Hz.
The active high time for each frequency is defined in the ACT_HIGH1..3 constants, and the number of cycles for each frequency with NCYCLES1..3
There are some calculations involved for CNTn and CNT_HIn. I will comment on them on the third part of the tutorial.
The core of the logic is a state machine. For each state, cyc1..3, the corresponding frequency is
generated. Three counters are used:
What I really don't like of this example is the repetition of a block of code for each state. There are several ways to solve this repetition (which is error prone). The one I selected will be presented on the next part of the tutorial.
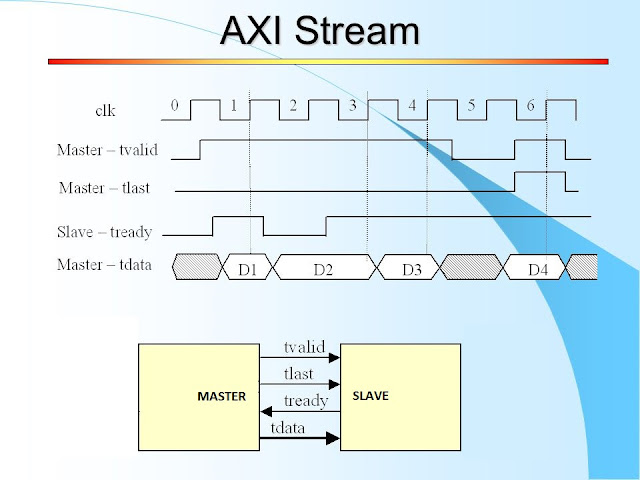
This is the waveform generated on the simulation:
It can be appreciated the number of cycles (3, 1, 2) generated for each frequency. Three cycles are generated for the fastest frequency, two cycles for the mid frequency, and one cycle for the slowest frequency.
The requirements for the project are to generate a sequence of square waveforms with different frequencies. For each frequency a number of cycles is generated (different for each one). For each frequency, a distinct duty cycle is also defined.
In this implementation the frequency is defined in Hz., and the active high time in ns. The VHDL code does not validate the parameters, i.e, if the active high time for any frequency is longer than its period, the output will be always '1' for that frequency. For each frequency, a number of cycles is defined.
This project was born over a discussion in Xilinx forums. Once I did the project for a specific configuration I started thinking about a way to make a generic solution, and this tutorial tries to reflect the design process of this small project.
The code is presented below. Three different frequencies FREQ1..3 are defined for this example, 242KHz, 23kHz and 57kHz. Notice that each frequency is defined in Hz.
The active high time for each frequency is defined in the ACT_HIGH1..3 constants, and the number of cycles for each frequency with NCYCLES1..3
There are some calculations involved for CNTn and CNT_HIn. I will comment on them on the third part of the tutorial.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 | library IEEE; use IEEE.STD_LOGIC_1164.ALL; use IEEE.NUMERIC_STD.ALL; use work.top_pkg.all; -- Uncomment the following library declaration if instantiating -- any Xilinx leaf cells in this code. --library UNISIM; --use UNISIM.VComponents.all; entity top is Port ( clk : in STD_LOGIC; reset : in STD_LOGIC; data_out : out STD_LOGIC ); end top; architecture Behavioral of top is -- Used for frequency generation constant FREQ1 : natural := 242720; -- in Hz constant FREQ2 : natural := 23600; constant FREQ3 : natural := 57400; constant CNT1 : natural := (10*SYS_FREQ/FREQ1 + 5)/10; constant CNT2 : natural := (10*SYS_FREQ/FREQ2 + 5)/10; constant CNT3 : natural := (10*SYS_FREQ/FREQ3 + 5)/10; -- Used for duty cycle of output signal constant ACT_HIGH1 : natural := 1200; -- in ns constant ACT_HIGH2 : natural := 15000; -- in ns constant ACT_HIGH3 : natural := 9000; -- in ns constant CNT_H1 : natural := (ACT_HIGH1*SYS_FREQ+5e8) / 1e9; constant CNT_H2 : natural := (ACT_HIGH2*SYS_FREQ+5e8) / 1e9; constant CNT_H3 : natural := (ACT_HIGH3*SYS_FREQ+5e8) / 1e9; constant NCYCLES1 : natural := 3; constant NCYCLES2 : natural := 1; constant NCYCLES3 : natural := 2; signal freq_cnt : unsigned(15 downto 0); signal act_cnt : unsigned(15 downto 0); signal cyc_cnt : unsigned(15 downto 0); type sm_type is (idle, cyc1, cyc2, cyc3); signal state : sm_type; begin seq_pr : process(clk) begin if (rising_edge(clk)) then if (reset = '1') then state <= idle; data_out <= '0'; else case(state) is when idle => freq_cnt <= to_unsigned(CNT1-1, 16); act_cnt <= to_unsigned(CNT_H1-1, 16); cyc_cnt <= to_unsigned(NCYCLES1-1, 16); data_out <= '1'; state <= cyc1; when cyc1 => -- Active high timing if (act_cnt = 0) then data_out <= '0'; else act_cnt <= act_cnt - 1; end if; -- Frequency and cycles if (freq_cnt = 0) then -- check number of cycles for this frequency data_out <= '1'; if (cyc_cnt = 0) then freq_cnt <= to_unsigned(CNT2-1, 16); act_cnt <= to_unsigned(CNT_H2-1, 16); cyc_cnt <= to_unsigned(NCYCLES2-1, 16); state <= cyc2; else cyc_cnt <= cyc_cnt - 1; freq_cnt <= to_unsigned(CNT1-1, 16); act_cnt <= to_unsigned(CNT_H1-1, 16); end if; else freq_cnt <= freq_cnt - 1; end if; when cyc2 => -- Active high timing if (act_cnt = 0) then data_out <= '0'; else act_cnt <= act_cnt - 1; end if; -- Frequency and cycles if (freq_cnt = 0) then -- check number of cycles for this frequency data_out <= '1'; if (cyc_cnt = 0) then freq_cnt <= to_unsigned(CNT3-1, 16); act_cnt <= to_unsigned(CNT_H3-1, 16); cyc_cnt <= to_unsigned(NCYCLES3-1, 16); state <= cyc3; else cyc_cnt <= cyc_cnt - 1; freq_cnt <= to_unsigned(CNT2-1, 16); act_cnt <= to_unsigned(CNT_H2-1, 16); end if; else freq_cnt <= freq_cnt - 1; end if; when cyc3 => -- Active high timing if (act_cnt = 0) then data_out <= '0'; else act_cnt <= act_cnt - 1; end if; if (freq_cnt = 0) then -- check number of cycles for this frequency data_out <= '1'; if (cyc_cnt = 0) then freq_cnt <= to_unsigned(CNT1-1, 16); act_cnt <= to_unsigned(CNT_H1-1, 16); cyc_cnt <= to_unsigned(NCYCLES1-1, 16); state <= cyc1; else cyc_cnt <= cyc_cnt - 1; freq_cnt <= to_unsigned(CNT3-1, 16); act_cnt <= to_unsigned(CNT_H3-1, 16); end if; else freq_cnt <= freq_cnt - 1; end if; when others => state <= idle; end case; end if; end if; end process seq_pr; end Behavioral; |
The core of the logic is a state machine. For each state, cyc1..3, the corresponding frequency is
generated. Three counters are used:
- cyc_cnt, to keep track of the number of cycles,
- act_cnt, to take care of the duty cycle of the waveform (how long it is '1', or active)
- and freq_cnt, to generate the frequency.
What I really don't like of this example is the repetition of a block of code for each state. There are several ways to solve this repetition (which is error prone). The one I selected will be presented on the next part of the tutorial.
This is the waveform generated on the simulation:
It can be appreciated the number of cycles (3, 1, 2) generated for each frequency. Three cycles are generated for the fastest frequency, two cycles for the mid frequency, and one cycle for the slowest frequency.
As always, the source code and test bench is available at Github




Comments
Post a Comment