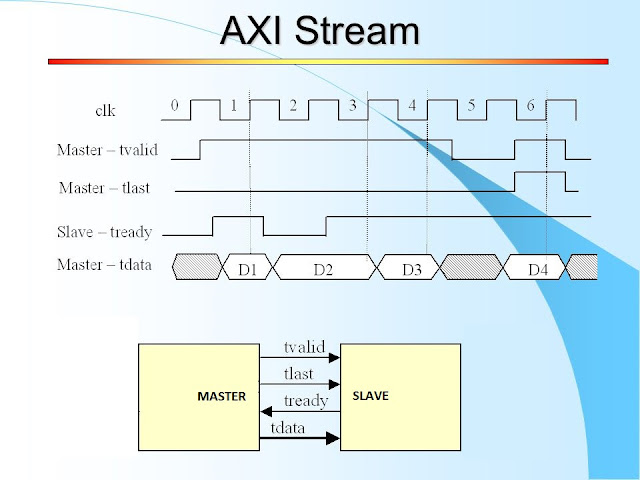
Pseudo random number generator Tutorial - Part 3

Matlab FFT of LFSR output

On the first two chapters of this Tutorial we started with a simple LFSR module and added a test bench. Then, on chapters three and four we upgraded our module with some features and learned to export the test bench data to files.

Chapter 5 - Matlab Formal Verification

Our VHDL block implements an algorithm that generates pseudo-random numbers. If the register is large enough, the output of the block will have hundreds or thousands of different numbers. How can we be sure that our block is working OK?

For algorithms validation, Matlab comes as a very handy tool. First, we will generate an LFSR in Matlab which also creates a results file. Then we can just simply compare both files, if they are equal, we have an additional degree of confidence in our VHDL block.

This is what the following Matlab code does:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

% Generate LFSR a = uint32(0); % Order of the polynom, up to 32 % Matlab range 1 to 32, VHDL 0 to 31 order = 16; av = zeros(2^order-1, 1); ii = 1; while (ii < 2^order) fb1 = bitxor(bitget(a, 15), bitget(a, 14)); fb2 = bitxor(bitget(a, 13), bitget(a, 6)); feedback = not( xor (fb1, fb2)); a = bitshift( a, 1, order) + uint32(feedback); av(ii, 1) = a; ii = ii + 1; end

The block is semi-configurable. It supports any register size up to 32. But you have to manually update lines 14, 15 and 16, which represent the feedback function to the LFSR and whose values can be taken from Xilinx's application note, page 5.

If you are like me, you may be asking yourself if this is enough. If we use the Matlab code to verify the LFSR, how can we know that it is OK? And how can we know that Xilinx's table is OK? After all, it could have a typo... Or maybe WE made a typo while copying from Xilinx table...

Being a little paranoid is good if you want to be a good design engineer. Doubt about everything. It is the way to find the bugs before your clients do that!

Well, in this case, I wrote some additional Matlab code to check the results. A good, or optimal, LFSR design, generates each and every number within its range (0 to 2^order - 1) just once.

So I wrote a little program to calculate how many times each LFSR generated number appears. If the block works well, each number will appear just once.

So, the maximum and the minimum of the 'y' vector will be one.

1 2 3 4 5 6 7 8 9 10

y = zeros(size(av)); for ii = 1:length(av) [rows] = find(av == (ii-1)); y(ii) = size(rows, 1); end max(y) min(y)

Let's put our tester' tester file to test. Suppose I copied the feedback function wrong and instead of '4' I wrote '6'. This is a sub-optimal LFSR that doesn't generate all possible values. When I ran the Matlab code between lines 22 and 31 I found that max(y)= 3 and min(y) = 0. Checking further, I found that, for example, value zero never happens, and value 1 happens three times:

Imagine trying to find those three values of '1' by looking into the file! There is no doubt that we must use tools (like co-simulation with Vivado and Matlab) to find these kind of perky bugs.

Chapter 6 - Matlab Data analysis

On Chapter 5 we did a great forward leap. We generated 'golden' data for our algorithm using Matlab (using a description of the algorithm and checking that the algorithm produces all the values for the order of our LFSR). Then we can compare the VHDL generated data with the 'golden' data and be sure that our VHDL algorithm performs well.

Matlab gives us many more advantages. It is a powerful tool that enables us to analyze data in many ways.

As we have said, the LFSR is a pseudo-random generator. So, how random is pseudo-random? Well, a really random generator will produce white noise. So let's make an FFT analysis of the LFSR produced data for different register sizes and see how close to pure noise they are.

For this purpose, I used the code below (Notice that the code analyzes 'res.log', i.e., the VHDL simulator output):

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

% Normalize the input m = (max(y)-min(y))/2; y1 = y/(y-m); Y = fft(y1,NFFT)/NFFT; f = linspace(0,1,NFFT/2+1); subplot % Plot single-sided amplitude spectrum. subplot(1,2,1); plot(f,20*log(abs(Y(1:NFFT/2+1)))) title('Single-Sided Amplitude Spectrum of y(t)') xlabel('Frequency (Hz)') ylabel('|Y(f)|') % Plot time domain subplot(1,2,2); plot(y1(1:250)); title('Time domain') xlabel('time')

And these are the results of running this Matlab code over the outputs for various LFSR sizes (5, 7, 9 and 11). The code graphs normalized amplitude vs. normalized frequency. It can be clearly seen that for small LFSR sizes the output is quite not random, while for LFSR=11, the output looks very close to white noise.

This is the last chapter of this tutorial. I hope that you enjoyed it and that it has given new ideas to improve your code and its verification.

The final release on Github (v1.3) for this tutorial includes the VHDL code and testbench, as well as the Maltab scripts used on these last chapters.