DTMF encoding and decoding
Dual Tone Multi-Frequency (DTMF) is a method for encoding and decoding up to sixteen digits and special characters to be sent over a voice channel.
DTMF was first developed by Bell Systems in United States, for use in push-button dialing telephones (in constrant to prior phones, which had a mechanic rotary dialing system).
DTMF is standardized by ITU-T Recommendation Q.23
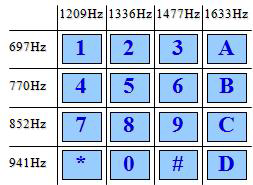
A DTMF keypad consists of a matrix of sixteen push buttons organized in four rows by four columns. Each button, when pressed, generates a pair of tones. The tones belong to two groups, a low frequency group (697 to 941 Hz) and a high frequency group (1209 to 1633 Hz). On the picture below you can see the buttons and associated frequencies:
Pressing an '8' generates two tones, one low frequency tone of 852 Hz and one high frequency tone of 1336Hz.
The frequencies were selected so no one would be an harmonic of another DTMF frequency.
As it usually is for many digital transmission systems, the encoder is quite simple while the decoder is much more complicated.
The decoder has to detect the presence of a pair of tones, but it has to filter out wide band signals like speech, which contain the frequencies of all the tones. The decoder must not only detect the presence of a pair of tones, but also the absence of any other pair. Many DTMF decoders also check the absence of the first harmonic of the detected pair of tones, to avoid confusing human voice with a DTMF tones pair.
Given what was described above, it is obvious that the receiver must make a frequency analysis of the received signal. But an FFT or DFT is a rather expensive algorithm. A preferred alternative is the Goertzel algorithm, which implements a bank of band pass filters in the frequencies of interest (the tone frequencies and, in some cases, their second harmonic).
I had the idea to publish this series of articles from a discussion on the FPGA projects group in Facebook. For the transmitter, an elegant solution is to use two NCOs to generate the two tones. A more straight forward solution is to use a square wave generator, each square wave belonging to one of the two groups.
I analyzed the behavior of a Goertzel based decoder on Matlab, for square wave and for sinusoidal tones, and I saw no real loss of detection capabilities for the square wave against the sinusoidal tones. On the following entries of these DTMF series I will explore tone generation using square waves, NCOs... and an intermediate option between the simple square waves and the more complex NCO based solution.
In the above figure, a comparison of the Matlab results of decoding sinusoidal tones against square tones. No degradation can be (easily) seen.
To make a sanity check, I also compared sinusoidal tones against sinusoidal tones with added noise. After adding (a lot of ) noise, it can be seen the degradation of the decoded signal:
The tone frequencies are still the strongest, but their relative power against those of the other detected frequencies is not so dominant. A threshold based detector would probably report no tones detected under these noise conditions.
DTMF was first developed by Bell Systems in United States, for use in push-button dialing telephones (in constrant to prior phones, which had a mechanic rotary dialing system).
DTMF is standardized by ITU-T Recommendation Q.23
A DTMF keypad consists of a matrix of sixteen push buttons organized in four rows by four columns. Each button, when pressed, generates a pair of tones. The tones belong to two groups, a low frequency group (697 to 941 Hz) and a high frequency group (1209 to 1633 Hz). On the picture below you can see the buttons and associated frequencies:
Pressing an '8' generates two tones, one low frequency tone of 852 Hz and one high frequency tone of 1336Hz.
The frequencies were selected so no one would be an harmonic of another DTMF frequency.
As it usually is for many digital transmission systems, the encoder is quite simple while the decoder is much more complicated.
The decoder has to detect the presence of a pair of tones, but it has to filter out wide band signals like speech, which contain the frequencies of all the tones. The decoder must not only detect the presence of a pair of tones, but also the absence of any other pair. Many DTMF decoders also check the absence of the first harmonic of the detected pair of tones, to avoid confusing human voice with a DTMF tones pair.
Given what was described above, it is obvious that the receiver must make a frequency analysis of the received signal. But an FFT or DFT is a rather expensive algorithm. A preferred alternative is the Goertzel algorithm, which implements a bank of band pass filters in the frequencies of interest (the tone frequencies and, in some cases, their second harmonic).
I had the idea to publish this series of articles from a discussion on the FPGA projects group in Facebook. For the transmitter, an elegant solution is to use two NCOs to generate the two tones. A more straight forward solution is to use a square wave generator, each square wave belonging to one of the two groups.
I analyzed the behavior of a Goertzel based decoder on Matlab, for square wave and for sinusoidal tones, and I saw no real loss of detection capabilities for the square wave against the sinusoidal tones. On the following entries of these DTMF series I will explore tone generation using square waves, NCOs... and an intermediate option between the simple square waves and the more complex NCO based solution.
In the above figure, a comparison of the Matlab results of decoding sinusoidal tones against square tones. No degradation can be (easily) seen.
To make a sanity check, I also compared sinusoidal tones against sinusoidal tones with added noise. After adding (a lot of ) noise, it can be seen the degradation of the decoded signal:
The tone frequencies are still the strongest, but their relative power against those of the other detected frequencies is not so dominant. A threshold based detector would probably report no tones detected under these noise conditions.




Comments
Post a Comment